Thin converging lenses

Any optical lens that is thicker in the middle than at the edges will make parallel light rays converge to a point, and is called converging lens.

How does the lens works? A lens produces its focusing effect because light travels more slowly in the lens than in the surrounding air, so that refraction of a light beam occurs at where the beam enters the lens and where it emerges from the lens into the air.

Main terms for lens:

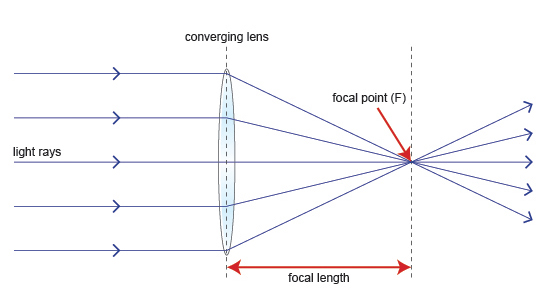
Focal length, f is the distance betwen the optical centre and the principal focus.

Optical centre is the point midway between the lens’ surfaces on its principal axis. Rays passing through the optical centre are not deviated.

Principal axis is the line passing symmetrically through the optical centre of the lens.

Focal point, F is the point to which all rays close to and incident parallel to the principal axis converge after refraction by the lens.

Focal plane is the plane which passes through the focal point and is perpendicular to the principal axis.

 

Thin converging lens

Thin lens are lens whose thickness is small compared to its focal length.

From the above image, it can be seen that light rays parallel to the principal axis will be focused on to the focal point. Light rays not parallel to the principal axis will be focused on to point along the focal plane.

 

Linear Magnification:

Linear magnification of a lens is defined as the ratio of the image height to the object height. It can be calculated using the equation below:

$m = \frac{h_{i}}{h_{o}} = \frac{v}{u}$

,where

• $h_{i}$ is the image height (height is the distance from the top of the image to the principal axis)
• $h_{o}$ is the object height (height is the distance from the top of the object to the principal axis)
• $v$ is the distance on the principal axis of the image from optical centre
• $u$ is the distance on the principal axis of the object from the optical centre