Assumption: Electromagnetic radiation is emitted in quanta and also absorbed in discrete units.
Since electrons are held by attractive forces to the atoms, to escape form a metal, an electron must do a certain amount of work to remove itself from the surface to infinity. An electron in a metal can only escape if it gains enough energy from a single photon to enable it to do the necessary work. So, individual photon must each supply more than a certain amount of energy.
The work function $\Phi$ of a material is defined as the minimum amount of the work necessary to remove a free electron from the surface of the material.
Einstein’s photoelectric equation: $E_{k \, max} = hf – \Phi$
- hf is the energy of the photon
- The electrons with maximum kinetic energy $E_{k \, max}$ come from the surface of the metal. Due to collisions with other atoms, those below the surface emerge with a ssmaller kinetic energy.
Threshold frequency is the minimum frequency of an incident radiation required to just remove an electron from the surface of a metal.
Threshold frequency( $f_{o}$) explained:
- Electrons can only escape if the maximum kinetic energy is greater than zero.
$\begin{aligned} E_{k \, max} &> 0 \\ hf – \Phi &> 0 \\ f_{o} &> \frac{\Phi}{h} \end{aligned}$
For photoelectric effect to take place, $f > f_{o}$.
Instantaneous emission of electrons explained:
- An electron is emitted if it gains enough energy from the photon. Since all photon energy is delivered immediately to the electron in a single collision, there is no time delay and is independent on the intensity of the incident radiation.
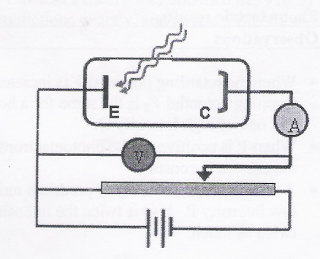
For a metal illuminated by electromagnetic wave,
- If the potential of E is held negative with respect to C, the photoelectrons escape more easily because they are repelled by the surface.
- But if potential of C is negative with respect to E, there exists a minimum negative potential required to stop even the most energetic electron from reaching electrode C.
The maximum kinetic energy $E_{k \, max}$ which a photoelectron can have:
$\begin{aligned} Loss \: in \: KE &= Gain \: in \: EPE \\ E_{k \, max} &= eV_{s} \\ &= \frac{1}{2} mv_{max}^{2} \\ &= eV_{s} \end{aligned}$
, where $V_{s}$ is the stopping potential
Substituting above equation into Einstein’s photoelectric equation,
$V_{s} = \frac{h}{e} f \, – \, \frac{\Phi}{e}$
what is threshold frequency?
what is impedance in LR circuit? Derive an expression for it.
nice work.would you please mind explaining stopping voltage.it confuses me
“But if potential of C is negative with respect to E, there exists a minimum negative potential required to stop even the most energetic electron from reaching electrode C.”
The minimum negative potential is the stopping voltage. When an electron is emitted from E, the electron possesses a certain amount of kinetic energy. As the electron travel from E to C, the electron loses kinetic energy and gain electric potential energy.
If the magnitude of the negative potential is large enough, the electron will lose ALL of its kinetic energy before it reaches electrode C (All the kinetic energy is converted to electric potential energy).
Note that the electrons ejected from electrode E will have a range of energy. The maximum energy that an electron ejected from the electrode can possess is determined by the frequency of the light shinning on the electrode E. The minimum negative potential will be the potential required to ensure that the maximum energy electrons just reaches electrode C.
Why does the electrons ejected from the electrode E have a range of energies?
This is because the electrons can undergo elastic collisions with the positively charged nucleus of other atoms, as the electrons are travelling out of the metal. Part of the kinetic energy of the colliding electron will be transferred to the nucleus.