Potential Barrier
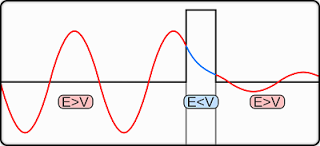
Consider an electron travelling along an ideal wire whose electric potential varies as shown below.
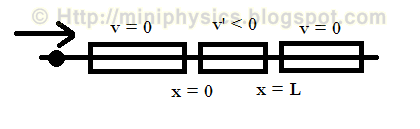
The negatively charged electron, which possesses an initial energy E, approaches the region (or ‘barrier’) of the wire, of width L, with negative potential. The electron is expected to gain electric potential energy of Uo = qv’ as it passes the region with negative potential.
By classical physics,
- if E > Uo, it is expected that the electron has sufficient energy to overcome the ‘potential varrier’ and will emerge from the right side of the wire.
- if E < Uo, it is expected that the electron did not have sufficient energy to over come the ‘potential barrier’ and would emerge again from the left side of the wire.
However, by quantum physics, since there is a wave function associated with the electron, the electron can emerge through (or tunnel through) the right side of the wire even when E < Uo.
The wave function associated with the electron must be continuous at the potential barrier and the wave function shows an exponential decay inside the potential barrier. Since the wave function must also be continuous on the right side of the potential barrier, there is a finite probability that the particle will tunnel through the potential barrier.
Recap: Classically, if electron does not have sufficient energy, it is not allowed to cross the potential barrier if the barrier energy is above the energy of the electron.
Short video on quantum tunnelling: