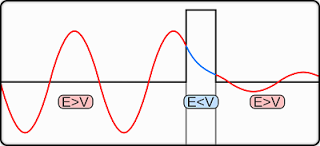
In the above diagram, the oscillating curve on the left of the potential barrier is a standing wave pattern that results from the interference between
- the incident matter wave and
- the reflected matter wave that has a smaller amplitude than the incident matter wave.
These two waves, of the same type, travelling in opposite directions interfere with each other thus setting up a standing wave pattern.
Within the potential barrier, the wave function decreases exponentially.
To the right of the potential barrier, the wave of lower amplitude but of the same energy as the incident matter wave emerges, indicating a small probability of detecting an electron in this region.
For a particle that tunnels through a potential barrier, a transmission coefficient T can be defined such that
$T = e^{-2kd}$
, where
- d = barrier thickness/width,
- $k = \sqrt{\frac{8 \pi^{2} m (U – E)}{h^{2}}}$, in which
- m = mass of particle
- U = potential energy of the potential barrier
- E = initial mechanical energy of the electron
- h = Planck’s constant.
The transmission coefficient T gives the probability which an approaching electron will be transmitted through the barrier (probability that tunnelling will occur).
Since T is an exponential function, its value is very much dependent on variables such as
- the mass m of the particle
- the barrier thickness
- the energy difference (U-E)
Since part of the incident matter wave will be transmitted and the other part reflected, a reflection coefficient R, which gives the probability which an approaching electron will be reflected, can also be defined such that
P(matter wave is reflected) R = 1 – P(matter wave is transmitted) T
Such that R + T = 1